Conţinut
Mișcare proiectilă se referă la mișcarea unei particule care este impartită cu o viteză inițială, dar care este ulterior supusă niciunei forțe în afară de cea a gravitației.
Aceasta include probleme în care o particulă este aruncată într-un unghi între 0 și 90 de grade față de orizontală, orizontală fiind de obicei solul. Pentru comoditate, se presupune că aceste proiectile călătoresc în (X y) avion, cu X reprezentând deplasarea orizontală și y deplasare verticală.
Calea parcursă de un proiectil este denumită a sa traiectorie. (Rețineți că legătura comună din „proiectil” și „traiectorie” este silaba „-ject”, „cuvântul latin pentru„ aruncă. „A scoate pe cineva înseamnă literalmente să-l arunce.) Punctul de origine al proiectilului în probleme în care trebuie să calculați traiectoria se presupune, de obicei, a fi (0, 0) pentru simplitate, dacă nu este specificat altfel.
Traiectoria unui proiectil este o parabolă (sau cel puțin urmărește o porțiune a unei parabole) dacă particulele sunt lansate în așa fel încât să aibă o componentă de mișcare orizontală nulă și nu există rezistență la aer să afecteze particulele.
Ecuațiile cinemice
Variabilele de interes în mișcarea unei particule sunt coordonatele de poziție ale acesteia X și y, viteza sa vși accelerarea acesteia A, totul în raport cu un timp dat T de la începutul problemei (când particulele sunt lansate sau eliberate). Rețineți că omiterea masei (m) implică faptul că gravitația pe Pământ acționează independent de această cantitate.
Rețineți, de asemenea, că aceste ecuații ignoră rolul rezistenței aerului, ceea ce creează o forță de tracțiune care se opune mișcării în situațiile reale ale Pământului. Acest factor este introdus în cursurile de mecanică la nivel superior.
Variabilele date cu un "0" subscript se referă la valoarea acelei cantități la timp T = 0 și sunt constante; adesea, această valoare este 0 datorită sistemului de coordonate ales, iar ecuația devine mult mai simplă. Accelerarea este tratată ca constantă în aceste probleme (și este în direcția y și egală cu -g, sau –9,8 m / s2, accelerația datorată gravitației în apropierea suprafeței Pământului).
Mișcare orizontală:
x = x0 + vX T
Mișcare verticală:
Exemple de mișcare proiectilă
Cheia pentru a putea rezolva probleme care includ calcule de traiectorie este de a ști că componentele orizontale (x) și verticale (y) ale mișcării pot fi analizate separat, așa cum este arătat mai sus, și contribuțiile lor respective la mișcarea generală rezumate perfect la sfârșitul problema.
Problemele de mișcare ale proiectilelor sunt considerate probleme de cădere liberă, deoarece, indiferent de aspectul lucrurilor, după timp T = 0, singura forță care acționează asupra obiectului în mișcare este gravitația.
Calcule traiectoriale
1. Cei mai rapizi ulciori din baseball pot arunca o minge la puțin peste 100 de mile pe oră sau 45 m / s. Dacă o minge este aruncată vertical în sus cu această viteză, cât de mare va ajunge și cât va dura pentru a reveni la punctul în care a fost eliberată?
Aici vy0 = 45 m / s, -g = –9,8 m / s, iar cantitățile de interes sunt înălțimea finală sau y, iar timpul total înapoi pe Pământ. Timpul total este un calcul în două părți: timpul până la y și timpul înapoi la y0 = 0. Pentru prima parte a problemei, vy, când mingea atinge înălțimea de vârf, este 0.
Începeți prin a folosi ecuația vy2 = v0Y2 - 2g (y - y0) și conectați valorile pe care le aveți:
0 = (45)2 - (2) (9.8) (y - 0) = 2.025 - 19.6y
y = 103,3 m
Ecuația vy = v0Y - gt arată că timpul t acest lucru este de (45 / 9.8) = 4,6 secunde. Pentru a obține timp total, adăugați această valoare la timpul necesar pentru ca mingea să cadă liber la punctul său de plecare. Acest lucru este dat de y = y0 + v0Yt - (1/2) gt2 , unde acum, pentru că mingea este încă în momentul în care începe să se prăbușească, v0Y = 0.
Rezolvare (103,3) = (1/2) gt2 pentru t dă t = 4.59 secunde.
Astfel, timpul total este de 4,59 + 4,59 = 9,18 secunde. Rezultatul poate surprinzător că fiecare „picior” al călătoriei, în sus și în jos, a dus în același timp subliniază faptul că gravitația este singura forță în joc aici.
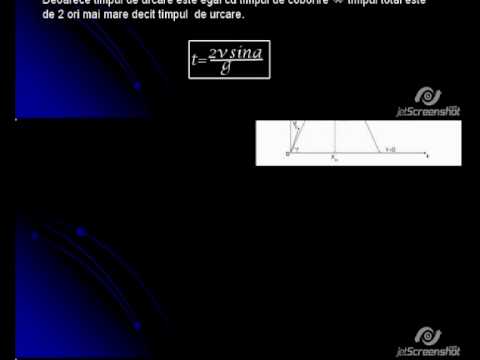
2. Ecuația intervalului: Când un proiectil este lansat cu viteză v0 și un unghi θ față de orizontală, are componente orizontale și verticale inițiale ale vitezei v0x = v0(cos θ) și v0Y = v0(păcat θ).
pentru că vy = v0Y - gt, și vy = 0 când proiectilul atinge înălțimea maximă, timpul până la înălțimea maximă este dat de t = v0Y/ G. Din cauza simetriei, va dura timpul pentru a reveni pe pământ (sau y = y0) este pur și simplu 2t = 2v0Y/g.
În cele din urmă, combinarea acestora cu relația x = v0xt, distanța orizontală parcursă având un unghi de lansare θ este
R (interval) = 2 (v02păcat θ ⋅ cos θ / g) = v02(Sin2θ) / g
(Etapa finală vine din identitatea trigonometrică 2 sinθ ⋅ cosθ = sin 2θ.)
Deoarece sin2θ are valoarea maximă de 1 când θ = 45 grade, folosind acest unghi se maximizează distanța orizontală pentru o viteză dată la
R = v02/ G.