
Conţinut
În geometrie, un octogon este un poligon cu opt laturi. Un octogon regulat are opt laturi egale și unghiuri egale. Octagonul obișnuit este recunoscut în mod obișnuit din semnele de oprire. Un octaedru este un poliedru cu opt fețe. Un octaedru obișnuit are opt triunghiuri cu margini de lungime egală. Este efectiv două piramidele pătrate care se întâlnesc la bazele lor.
Formula zonei Octagon
Formula pentru aria unui octogon obișnuit cu laturile de lungime "a" este 2 (1 + sqrt (2)) a ^ 2, unde "sqrt" indică rădăcina pătrată.
Derivare
Un octogon poate fi privit ca 4 dreptunghiuri, un pătrat în centru și patru triunghiuri izoscele în colțuri.
Pătratul este de suprafață a ^ 2.
Triunghiurile au laturile a, a / sqrt (2) și / sqrt (2), de teorema pitagoreică. Prin urmare, fiecare are o suprafață de a ^ 2/4.
Dreptunghiurile sunt din aria a * a / sqrt (2).
Suma acestor 9 zone este 2a ^ 2 (1 + sqrt (2)).
Formula volumului octaedru
Formula pentru volumul unui octaedru obișnuit de laturi "a" este un ^ 3 * sqrt (2) / 3.
Derivare
Zona unei piramide pe patru fețe este aria bazei * înălțime / 3. Suprafața unui octogon obișnuit este de aceea 2 * bază * înălțime / 3.
Baza = a ^ 2 trivial.
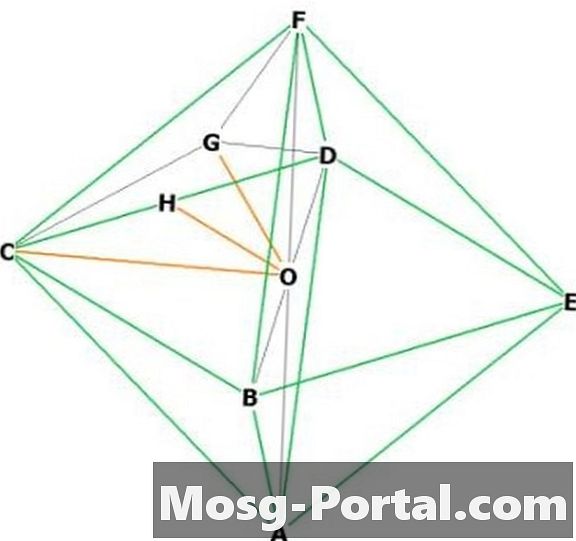
Alegeți două vârfuri adiacente, spuneți „F” și „C.” „O” este în centru. FOC este un triunghi izoscel drept cu baza "a", deci OC și OF au lungimea a / sqrt (2) de teorema pitagoreică. Deci înălțime = a / sqrt (2).
Deci volumul unui octaedru obișnuit este de 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Suprafață
Suprafața regulată a octaedrelor este aria unui triunghi echilateral al laturii „a” ori de 8 fețe.
Pentru a utiliza teorema lui Pitagore, aruncați o linie de la vârf la bază. Aceasta creează două triunghiuri drepte, cu ipotenuză lungimea „a” și lungimea latură „a / 2”. Prin urmare, a treia latură trebuie să fie sqrt = sqrt (3) a / 2. Deci aria unui triunghi echilateral este înălțimea * bază / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
Cu 8 laturi, suprafața unui octaedru obișnuit este de 2 * sqrt (3) * a ^ 2.