
Conţinut
Pentru ca două forme să fie congruente, fiecare trebuie să aibă același număr de laturi, iar unghiurile lor trebuie să fie la fel. Cele mai simple metode de a determina dacă două forme sunt congruente este de a roti una dintre forme până când este aliniată cu cealaltă, sau pur și simplu stivați formele una peste alta pentru a vedea dacă vreun capăt se lipeste. Dacă nu puteți muta formele fizic, puteți utiliza formule pentru a determina dacă formele sunt congruente.
Cercuri congruente
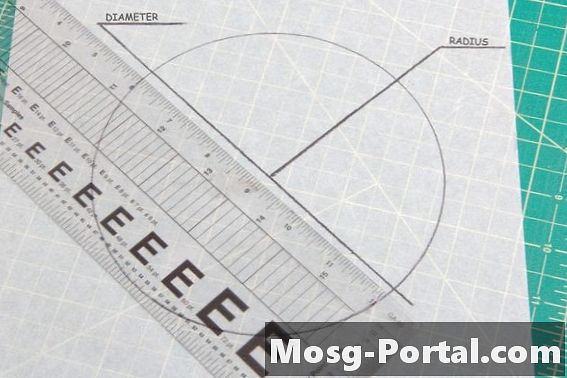
••• Ray Robert Green / Demand MediaToate cercurile au același unghi de 360 de grade. Singurul factor în determinarea congruenței a două cercuri este compararea dimensiunii acestora. Diametrul este o linie dreaptă prin centrul cercului de la margine la margine, în timp ce raza unui cerc este lungimea de la centrul său la marginea exterioară. Măsurarea oricăruia dintre acestea pe ambele cercuri va demonstra dacă sunt congruente.
paralelograme
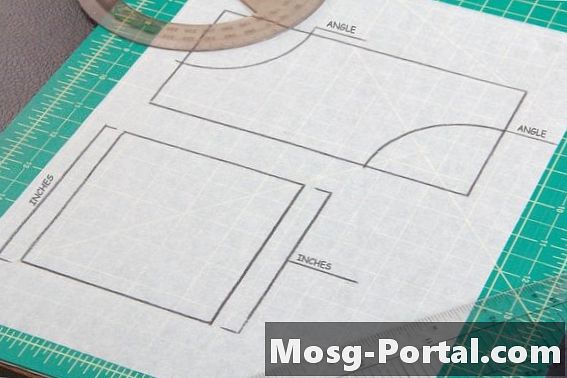
O paralelogramă are două perechi de laturi paralele, cum ar fi pătrate și dreptunghiuri. Părțile sau unghiurile opuse ale unui paralelogram au aceeași măsură, deci este necesar să se efectueze două măsurători de unghi sau lateral pe o paralelogramă, una din fiecare pereche de laturi, pentru a compara congruența cu o altă formă.
triunghiurile
••• Ray Robert Green / Demand MediaPentru a găsi congruența triunghiurilor, trebuie să determinați dimensiunea fiecărui unghi sau latură, deoarece toate cele trei pot fi diferite. Există trei postulate care pot fi utilizate pentru identificarea triunghiurilor congruente. Postulatul SSS este atunci când măsurați toate cele trei laturi la fiecare triunghi. Postulatul ASA spune că dacă două unghiuri și latura lor de legătură se potrivesc cu cea a celuilalt triunghi, atunci sunt congruente. Postulul SAS face opusul, măsurând două laturi și unghiul lor de legătură pentru a se compara cu celălalt triunghi.
Teoreme pentru triunghiuri congruente

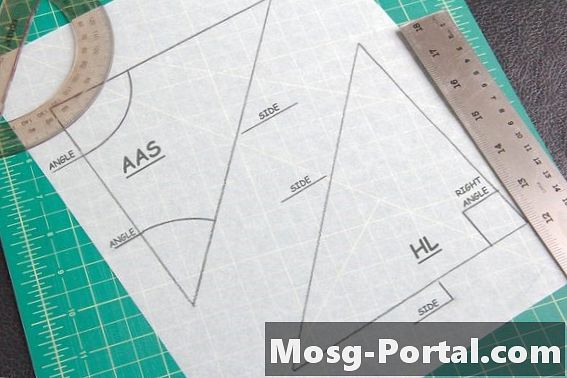
Două teoreme sunt utile pentru găsirea triunghiurilor congruente. Teorema AAS spune că dacă două unghiuri și o latură care nu leagă cele două sunt egale cu cea a unui alt triunghi, atunci ele sunt congruente. Teorema Hypotenuse-Leg se aplică numai triunghiurilor cu un unghi de 90 de grade sau „drept”. Acest lucru este atunci când măsurați ipotenuză - latura opusă unghiului de 90 de grade - și una dintre celelalte laturi ale triunghiului, pentru a compara cu cealaltă formă.