Conţinut
Toate triunghiurile drepte au unghiuri de 90 de grade sau drepte. Sunt utilizate în matematică pentru calcule speciale, inclusiv găsirea distanței exacte între două puncte. Triunghiurile drepte vă pot ajuta, de asemenea, să găsiți înălțimi și distanțe foarte mari sau altfel greu de măsurat. Triunghiurile drepte au multe proprietăți speciale care stau la baza trigonometriei.
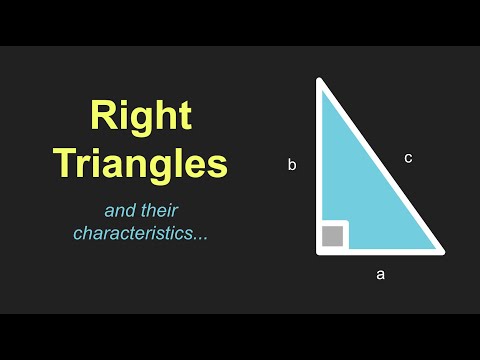
Anatomia unui triunghi drept
Cele două laturi mai scurte ale unui unghi drept se numesc picioare. De obicei, acestea sunt etichetate cu literele „a” și „b.” A treia latură, care este opusă unghiului de 90 de grade, se numește hipotenuză și este de obicei etichetată „c”.
Teorema lui Pitagora
Teorema pitagoreă afirmă că suma fiecăruia dintre lungimile dreptunghiului unui triunghi dreptunghiular este egală cu lungimea hipotenuzei pătrate. Cu alte cuvinte, a ^ 2 + b ^ 2 = c ^ 2, unde "a" și "b" sunt picioare și "c" este hipotenuză. Dacă cunoașteți două laturi ale unui triunghi drept, teorema poate fi aplicată pentru a găsi a treia latură. Acest lucru este utilizat în multe cazuri pentru a găsi distanțe sau lungimi greu de măsurat. De exemplu, dacă știți că conduceți 10 blocuri spre sud, apoi 6 blocuri spre est pentru a ajunge de la casă la magazin, dar doriți să știți care este distanța directă dintre casă și magazin. Puteți configura 10 ^ 2 + 6 ^ 2 = (distanța directă) ^ 2 pentru a afla că este vorba de aproximativ 12 blocuri pe măsură ce zboară ploaia.
45-45-90 Triunghiuri
Unul dintre triunghiurile speciale drepte este triunghiul 45-45-90. Se formează prin trasarea unei linii diagonale de la un colț la colțul opus al unui pătrat. Este singurul triunghi drept unde ambele picioare măsoară exact aceeași lungime. Astfel, este singurul tip de triunghi drept care este și un triunghi izoscel. Numele 45-45-90 provine de la măsurile unghiurilor sale interioare. Există unghiul necesar 90 de grade, iar unghiurile mai mici ambele măsoară 45 de grade. Picioarele și hipotenuză afișează întotdeauna un raport 1: √2. Astfel, pentru acest triunghi trebuie doar să cunoașteți lungimea unei părți pentru a găsi celelalte două lungimi. Lungimile picioarelor sunt egale, iar lungimea hipotenuzei este egală cu lungimea unui picior √2.
30-60-90 Triunghiuri
Ca și în cazul triunghiului 45-45-90, triunghiul 30-60-90 își primește numele, deoarece unghiurile interioare măsoară 30, 60 și 90 de grade. Acest triunghi este format prin tăierea unui triunghi echilateral în jumătate. Laturile triunghiurilor 30-60-90 formează, de asemenea, un raport constant de 1: √3: 2. Piciorul scurt este direct vizavi de unghiul de 30 de grade și măsoară întotdeauna jumătate din lungimea hipotenuzei, care este față de Unghi de 90 de grade. Piciorul mai lung, care se află peste unghiul de 60 de grade, măsoară lungimea timpului scurt √3 sau jumătate din timpii de ipotenuză √3. Astfel, pentru acest triunghi trebuie să știți doar lungimea unei părți pentru a găsi lungimile celorlalte două fețe.