Conţinut
- TL; DR (Prea lung; nu a citit)
- Frecvența naturală a unui oscilator armonic simplu definit
- Calcularea frecvenței naturale
Toate mișcările oscilante - mișcarea unei coarde de chitară, o tijă care vibrează după ce a fost lovită sau săriturile unei greutăți pe un arc - au o frecvență naturală. Situația de bază pentru calcul implică o masă pe un arc, care este un simplu oscilator armonic. Pentru cazuri mai complicate, puteți adăuga efectele amortizării (încetinirea oscilațiilor) sau puteți construi modele detaliate cu forțe motrice sau alți factori luați în considerare. Cu toate acestea, calcularea frecvenței naturale pentru un sistem simplu este ușoară.
TL; DR (Prea lung; nu a citit)
Calculați frecvența naturală a unui oscilator armonic simplu folosind formula:
f = √(k / m) ÷ 2π
Introduceți constantă de primăvară pentru sistemul pe care îl considerați la fața locului k, și masa oscilantă pentru mși apoi evaluați.
Frecvența naturală a unui oscilator armonic simplu definit
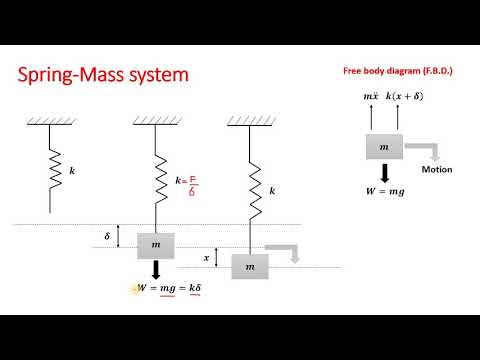
Imaginează-ți un izvor cu o bilă fixată la capăt cu masă m. Când configurația este staționară, arcul este parțial întins, iar întreaga configurație este în poziția de echilibru, unde tensiunea din arcul extins se potrivește cu forța gravitației trăgând mingea în jos. Îndepărtarea mingii de această poziție de echilibru fie adaugă tensiune arcului (dacă o întinzi în jos), fie dă gravitației posibilitatea de a trage mingea în jos, fără ca tensiunea de la arc să o contracareze (dacă împingeți mingea în sus). În ambele cazuri, mingea începe să oscileze în jurul poziției de echilibru.
Frecvența naturală este frecvența acestei oscilații, măsurată în hertz (Hz). Acest lucru vă spune câte oscilații se întâmplă pe secundă, care depinde de proprietățile arcului și de masa bilei atașate de acesta. Șiruri de chitară, tije lovite de un obiect și multe alte sisteme oscilează la o frecvență naturală.
Calcularea frecvenței naturale
Următoarea expresie definește frecvența naturală a unui oscilator armonic simplu:
f = ω /2π
Unde ω este frecvența unghiulară a oscilației, măsurată în radiani / secundă. Următoarea expresie definește frecvența unghiulară:
ω = √(k / m)
Deci aceasta înseamnă:
f = √(k / m) ÷ 2π
Aici, k este constantă de izvor pentru primăvara în cauză și m este masa mingii. Constanta de arc este măsurată în Newtoni / metru. Izvoarele cu constante mai mari sunt mai rigide si ia mai multa forta pentru a se extinde.
Pentru a calcula frecvența naturală folosind ecuația de mai sus, aflați mai întâi constanta de arc pentru sistemul dvs. specific. Puteți găsi constanta de primăvară pentru sistemele reale prin experimentare, dar pentru cele mai multe probleme, vi se oferă o valoare pentru aceasta. Introduceți această valoare la fața locului k (în acest exemplu, k = 100 N / m) și împărțiți-l după masa obiectului (de exemplu, m = 1 kg). Apoi, luați rădăcina pătrată a rezultatului, înainte de a împărți acest lucru cu 2π. Parcurgând pașii:
f = √ (100 N / m / 1 kg) ÷ 2π
= √ (100 s.)−2) ÷ 2π
= 10 Hz ÷ 2π
= 1,6 Hz
În acest caz, frecvența naturală este de 1,6 Hz, ceea ce înseamnă că sistemul ar oscila puțin de o dată și jumătate pe secundă.