Conţinut
Suprafețele exercită o forță de frecare care rezistă mișcărilor culisante și trebuie să calculați dimensiunea acestei forțe ca parte a multor probleme de fizică. Cantitatea de frecare depinde în principal de „forța normală”, care suprafețele exercită asupra obiectelor care stau pe ele, precum și de caracteristicile suprafeței specifice pe care o luați în considerare. În cele mai multe scopuri, puteți utiliza formula F = μN pentru a calcula frecarea, cu N în fața forței „normale” și „μ”Încorporând caracteristicile suprafeței.
TL; DR (Prea lung; nu a citit)
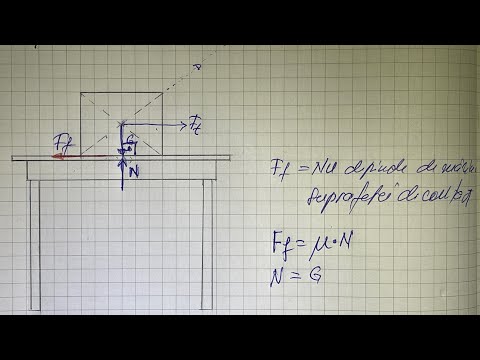
Calculați forța de frecare folosind formula:
F = μN
Unde N este forța normală și μ este coeficientul de frecare al materialelor dvs. și dacă acestea sunt staționare sau în mișcare. Forța normală este egală cu greutatea obiectului, deci se poate scrie și:
F = μmg
Unde m este masa obiectului și g este accelerația datorată gravitației. Fricțiunea acționează pentru a se opune mișcării obiectului.
Ce este frecarea?
Fricțiunea descrie forța dintre două suprafețe atunci când încercați să vă deplasați una peste alta. Forța rezistă mișcării și, în cele mai multe cazuri, forța acționează în direcția opusă mișcării. În jos, la nivel molecular, când apăsați două suprafețe împreună, imperfecțiuni minore în fiecare suprafață se pot interbloca și pot exista forțe atractive între moleculele unui material și celălalt. Acești factori îngreunează trecerea lor unul peste altul. Nu lucrați la acest nivel atunci când calculați forța de frecare. Pentru situațiile de zi cu zi, fizicienii grupează toți acești factori împreună în „coeficientul” μ.
Calcularea forței de frecare
Forța „normală” descrie forța pe care suprafața pe care se sprijină (sau este apăsat pe) o exercită asupra obiectului. Pentru un obiect nemișcat pe o suprafață plană, forța trebuie să se opună exact forței datorită gravitației, altfel obiectul s-ar muta, în conformitate cu legile mișcării lui Newton. Forța „normală” (N) este numele forței care face acest lucru.
Acționează întotdeauna perpendicular pe suprafață. Acest lucru înseamnă că pe o suprafață înclinată, forța normală ar indica în continuare direct distanță de suprafață, în timp ce forța gravitației ar îndrepta direct în jos.
Forța normală poate fi pur și simplu descrisă în majoritatea cazurilor de:
N = mg
Aici, m reprezintă masa obiectului și g reprezintă accelerația datorată gravitației, care este de 9,8 metri pe secundă pe secundă (m / s)2) sau neturi pe kilogram (N / kg). Acest lucru se potrivește pur și simplu cu „greutatea” obiectului.
Pentru suprafețele înclinate, rezistența forței normale este redusă cu cât suprafața este înclinată, deci formula devine:
N = mg cos (θ)
Cu θ stând pentru unghiul la care este înclinată suprafața.
Pentru un exemplu simplu de calcul, luați în considerare o suprafață plană cu un bloc de lemn de 2 kg așezat pe ea. Forța normală ar îndrepta direct în sus (pentru a susține greutatea blocului), și ați calcula:
N = 2 kg × 9,8 N / kg = 19,6 N
Coeficientul depinde de obiectul și situația specifică cu care lucrați. Dacă obiectul nu se deplasează deja pe suprafață, utilizați coeficientul de frecare statică μstatic, dar dacă se mișcă, utilizați coeficientul de frecare glisantă μdiapozitiv.
În general, coeficientul de frecare glisant este mai mic decât coeficientul de frecare statică. Cu alte cuvinte, este mai ușor să glisați ceva care deja glisează decât să glisați ceva care este încă.
Materialele pe care le considerați afectează și coeficientul. De exemplu, dacă blocul de lemn de mai devreme s-a aflat pe o suprafață de cărămidă, coeficientul ar fi de 0,6, dar pentru lemnul curat poate fi oriunde între 0,25 și 0,5. Pentru gheața pe gheață, coeficientul static este 0,1. Din nou, coeficientul de alunecare reduce și mai mult acest lucru, la 0,03 pentru gheață pe gheață și 0,2 pentru lemn pe lemn. Căutați aceste suprafețe cu ajutorul unui tabel online (consultați Resurse).
Formula forței de frecare prevede:
F = μN
De exemplu, luați în considerare un bloc de lemn cu o greutate de 2 kg pe o masă de lemn, fiind împins de la staționare. În acest caz, utilizați coeficientul static, cu μstatic = 0,25 la 0,5 pentru lemn. luare μstatic = 0,5 pentru a maximiza efectul potențial de frecare și amintirea N = 19,6 N de mai devreme, forța este:
F = 0,5 × 19,6 N = 9,8 N
Amintiți-vă că frecarea nu oferă decât forța de a rezista mișcării, așa că dacă începeți să o împingeți ușor și să faceți mai ferm, forța de frecare va crește până la o valoare maximă, ceea ce tocmai ați calculat. Fizicienii scriu uneori Fmax pentru a clarifica acest punct.
Odată ce blocul se mișcă, utilizați μdiapozitiv = 0,2, în acest caz:
Fdiapozitiv = μdiapozitiv N
= 0,2 × 19,6 N = 3,92 N