
Autocorelația este o metodă statistică folosită pentru analiza seriilor de timp. Scopul este măsurarea corelației a două valori în același set de date la pași de timp diferiți. Deși datele de timp nu sunt folosite pentru calcularea autocorelației, creșterile de timp trebuie să fie egale pentru a obține rezultate semnificative. Coeficientul de autocorelare are două scopuri. Poate detecta non-aleatoriu într-un set de date. Dacă valorile din setul de date nu sunt aleatorii, atunci autocorelarea poate ajuta analistul să aleagă un model de serie de timp adecvat.
Calculați media, sau media, pentru datele pe care le analizați. Media este suma tuturor valorilor de date împărțită la numărul de valori de date (n).
Decideți un interval de timp (k) pentru calculul dvs. Valoarea de întârziere este un număr întreg care indică câți pași de timp separă o valoare de alta. De exemplu, decalajul dintre (y1, t1) și (y6, t6) este de cinci, deoarece există 6 - 1 = 5 pași de timp între cele două valori. Atunci când testezi aleatoriu, de obicei, vei calcula doar un coeficient de autocorelație folosind lag k = 1, deși alte valori de lag vor funcționa și ele. Când stabiliți un model de serie temporală adecvat, va trebui să calculați o serie de valori de autocorelație, utilizând o valoare diferită pentru fiecare.
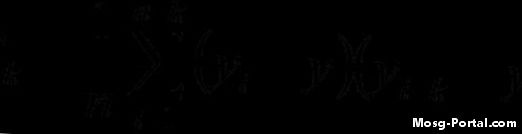
Calculați funcția de autocovarianță folosind formula dată. De exemplu, calculați a treia iterație (i = 3) folosind un lag k = 7, atunci calculul pentru această iterație ar arăta astfel: (y3 - y-bar) (y10 - y-bar) Iterate prin toate valorile „i” și apoi luați suma și împărțiți-o după numărul de valori din setul de date.
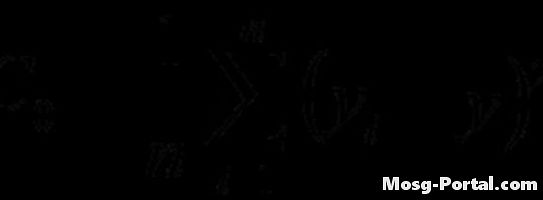
Calculați funcția de varianță folosind formula dată. Calculul este similar cu cel al funcției de autocovarianță, dar lag nu este utilizat.

Împărțiți funcția de autocovarianță la funcția de varianță pentru a obține coeficientul de autocorelare. Puteți evita acest pas împărțind formulele pentru cele două funcții așa cum este arătat, dar de multe ori, veți avea nevoie de autocovarianță și variație în alte scopuri, de aceea este practic să le calculați și individual.