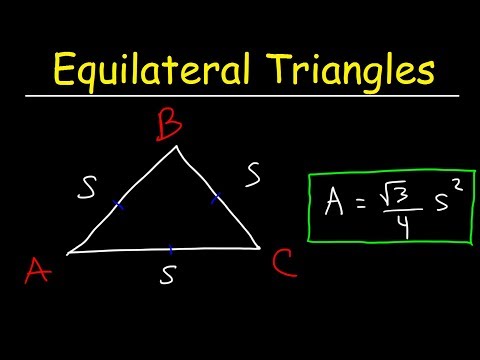
Un triunghi echilateral este un triunghi cu toate cele trei laturi de lungime egală. Suprafața unui poligon bidimensional, cum ar fi un triunghi, este suprafața totală conținută de laturile poligonului. Cele trei unghiuri ale unui triunghi echilateral sunt, de asemenea, de măsură egală în geometria euclidiană. Deoarece măsura totală a unghiurilor unui triunghi euclidian este de 180 de grade, acest lucru înseamnă că unghiurile unui triunghi echilateral măsoară toate 60 de grade. Zona unui triunghi echilateral poate fi calculată atunci când lungimea unuia dintre laturile sale este cunoscută.

Determinați zona unui triunghi atunci când baza și înălțimea sunt cunoscute. Luăm orice triunghi identic cu baza s și înălțimea h. Cu aceste două triunghiuri putem forma întotdeauna un paralelogram de bază s și înălțime h. Deoarece aria unei paralelograme este s x h, aria A a unui triunghi este, prin urmare, ½ s x h.

Formați triunghiul echilateral în două triunghiuri drepte cu segmentul de linie h. Hipotenuză a unuia dintre aceste triunghiuri drepte lungime, unul dintre picioare are lungimea h, iar celălalt picior are lungimea s / 2.
Exprimă h în termeni de s. Folosind triunghiul format în pasul 2, știm că s ^ 2 = (s / 2) ^ 2 + h ^ 2 prin formula pitagoreică. Prin urmare, h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, iar acum avem h = (3 ^ 1/2) s / 2.
Se înlocuiește valoarea lui h obținută în etapa 3 în formula unei zone de triunghiuri obținute la pasul 1. Deoarece A = ½ sxh și h = (3 ^ 1/2) s / 2, acum avem A = ½ s (3 ^ 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Utilizați formula pentru aria unui triunghi echilateral obținut la pasul 4 pentru a găsi aria unui triunghi echilateral cu laturile de lungime 2. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).