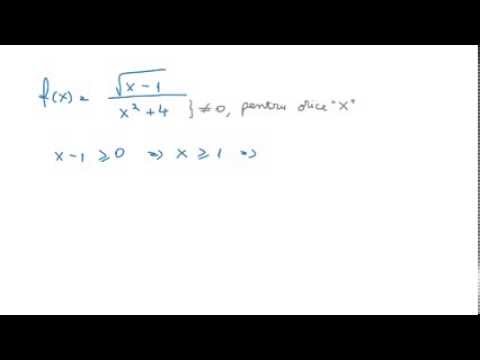
Conţinut
- Strategia pentru găsirea domeniului
- Un exemplu de găsire a domeniului
- Un alt exemplu de găsire a domeniului
Când începeți să aflați prima dată despre funcții, poate fi necesar să le considerați ca o mașină: introduceți o valoare, X, în funcție, și odată procesată prin aparat, o altă valoare - permite apelarea acesteia y - iese la iveală. Gama posibilă X intrările care pot veni prin aparat pentru a returna o ieșire validă se numește domeniul funcției. Așadar, dacă vi se cere să găsiți domeniul unei funcții, trebuie să aflați cu adevărat care intrări posibile ar putea returna o ieșire valabilă.
Strategia pentru găsirea domeniului
Dacă aflați doar despre funcții și domenii, de obicei se presupune că un domeniu al funcțiilor este „toate numerele reale”. Așadar, atunci când stabiliți definirea domeniului, este cel mai adesea cel mai ușor să vă folosiți cunoștințele de matematică - în special algebra - pentru a determina ce numere arent membri valabili ai domeniului. Deci, atunci când vedeți instrucțiunile „găsiți domeniul”, este cel mai adesea cel mai ușor să le citiți în capul dvs. ca „să găsiți și să eliminați orice numere care supraînălțare fii în domeniu ".
În cele mai multe cazuri, acest lucru se reduce la verificarea (și eliminarea) intrărilor potențiale care ar face ca fracțiile să devină nedefinite sau să aibă 0 în numitorul lor și să caute intrări potențiale care să vă ofere numere negative sub un semn rădăcină pătrată.
Un exemplu de găsire a domeniului
Luați în considerare funcția f(X) = 3/(X - 2), ceea ce înseamnă cu adevărat că orice număr introdus va fi redus în loc de X în partea dreaptă a ecuației. De exemplu, dacă ați calculat f(4) ai fi avut f(4) = 3 / (4 - 2), care se rezolvă la 3/2.
Dar dacă ai calcula f(2) sau, cu alte cuvinte, introducerea 2 în locul X? Atunci ai fi avut f(2) = 3 / (2 - 2), care se simplifică până la 3/0, care este o fracție nedefinită.
Aceasta ilustrează una dintre cele două instanțe comune care pot exclude un număr din domeniul unei funcții. Dacă există o fracție implicată și intrarea ar face ca numitorul fracției să fie zero, atunci intrarea trebuie exclusă din domeniul funcțiilor.
Un mic examen vă va arăta că absolut orice număr cu exceptia 2 va întoarce un rezultat valid (dacă uneori dezordonat) pentru funcția în cauză, deci domeniul acestei funcții este toate numerele, cu excepția celor 2.
Un alt exemplu de găsire a domeniului
Există o altă instanță comună care va exclude posibilii membri ai unui domeniu de funcții: având o cantitate negativă sub un semn rădăcină pătrată sau orice radical cu un index egal. Luați în considerare funcția de exemplu f(X) = √(5 - X).
Dacă X ≤ 5, atunci cantitatea de sub semnul radical va fi 0 sau pozitivă și va returna un rezultat valid. De exemplu, dacă X = 4,5 ai avea f(4.5) = √ (5 - 4.5) = √ (.5) care, deși dezordonat, returnează în continuare un rezultat valid. Si daca X = -10 ai avea f(4.5) = √ (5 - (-10)) = √ (5 + 10) = √ (15 care, din nou, returnează un rezultat valabil, dacă este dezordonat).
Dar imaginați-vă că X = 5.1. În momentul în care treceți peste linia de împărțire între 5 și orice numere mai mari decât aceasta, ajungeți cu un număr negativ sub radical:
f(5.1) = √(5 - 5.1) = √(-.1)
Mult mai târziu în cariera de matematică, veți învăța să faceți sensul rădăcinilor pătrate negative folosind un concept numit imagini numere sau numere complexe. Însă, deocamdată, având un număr negativ sub semnul radical exclude această intrare ca membru valid al domeniului funcțiilor.
Deci, în acest caz, pentru că orice număr X ≤ 5 returnează un rezultat valid pentru această funcție și orice număr X > 5 returnează un rezultat nevalid, domeniul funcției este toate numerele X ≤ 5.