Conţinut
- TL; DR (Prea lung; nu a citit)
- Ce este forța centripetă?
- Formula pentru forța centripetă și accelerarea centripetară
- sfaturi
- Găsirea forței centripete cu informații incomplete
Orice obiect care se mișcă într-un cerc se accelerează, chiar dacă viteza acestuia rămâne aceeași. Acest lucru poate părea contraintuativ, deoarece cum poți avea accelerație fără o schimbare a vitezei? De fapt, deoarece accelerația este viteza de schimbare a vitezei, iar viteza include viteza și direcția de mișcare, este imposibil să aveți mișcare circulară fără accelerație. Prin a doua lege a lui Newton, orice accelerare (A) este legat de o forță (F) de F = ma, iar în cazul mișcării circulare, forța în cauză se numește forță centripetă. Elaborarea acestui lucru este un proces simplu, dar poate fi necesar să vă gândiți la situație în moduri diferite, în funcție de informațiile pe care le aveți.
TL; DR (Prea lung; nu a citit)
Găsiți forța centripetă folosind formula:
F = mv2 / r
Aici, F face referire la forță, m este masa obiectului, v este viteza tangențială a obiectului și r este raza cercului în care călătorește. Dacă știți sursa forței centripetale (gravitația, de exemplu), puteți găsi forța centripetă folosind ecuația pentru această forță.
Ce este forța centripetă?
Forța centripetă nu este o forță în același mod ca forța gravitațională sau forța de frecare. Forța centripetă există deoarece există accelerația centripetală, dar cauza fizică a acestei forțe poate varia în funcție de situația specifică.
Luați în considerare mișcarea Pământului în jurul soarelui. Chiar dacă viteza orbitei sale este constantă, schimbă direcția continuu și, prin urmare, are accelerație îndreptată spre soare. Această accelerație trebuie să fie cauzată de o forță, în conformitate cu primele și a doua legi de mișcare ale lui Newton. În cazul orbitei Pământului, forța care provoacă accelerația este gravitația.
Cu toate acestea, dacă balansați o minge pe o sfoară într-un cerc la o viteză constantă, forța care provoacă accelerația este diferită. În acest caz, forța provine din tensiunea din coardă. Un alt exemplu este o mașină care menține o viteză constantă, dar care se rotește în cerc. În acest caz, frecarea dintre roțile mașinii și drum este sursa forței.
Cu alte cuvinte, forțele centripete există, dar cauza fizică a acestora depinde de situație.
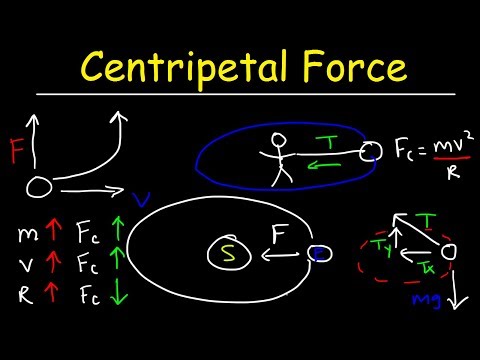
Formula pentru forța centripetă și accelerarea centripetară
Accelerația centripetă este denumirea pentru accelerație direct spre centrul cercului în mișcare circulară. Aceasta este definită de:
A = v2 / r
Unde v este viteza obiectului din linia tangențială a cercului și r este raza cercului în care se deplasează. Gândiți-vă ce s-ar întâmpla dacă ați balansa o bilă conectată la un șir într-un cerc, dar șirul s-a rupt. Mingea ar zbura în linie dreaptă din poziția sa pe cerc în momentul în care s-a rupt șirul, iar asta vă oferă o idee ce v înseamnă în ecuația de mai sus.
Deoarece a doua lege a lui Newton afirmă că forța = masa × accelerarea și avem o ecuație pentru accelerație deasupra, forța centripetă trebuie să fie:
F = mv2 / r
În această ecuație, m se referă la masă.
Deci, pentru a găsi forța centripetă, trebuie să cunoașteți masa obiectului, raza cercului în care călătorește și viteza tangențială a acestuia. Folosiți ecuația de mai sus pentru a găsi forța bazată pe acești factori. Pătrate viteza, înmulțiți-o cu masa și apoi împărțiți rezultatul pe raza cercului.
sfaturi
Găsirea forței centripete cu informații incomplete
Dacă nu aveți toate informațiile de care aveți nevoie pentru ecuația de mai sus, s-ar putea părea că găsirea forței centripete este imposibilă. Cu toate acestea, dacă vă gândiți la situație, puteți de multe ori să aflați care ar putea fi forța.
De exemplu, dacă încercați să găsiți forța centripetă care acționează pe o planetă orbitând pe o stea sau pe o lună care orbitează pe o planetă, știți că forța centripetă provine din gravitație. Aceasta înseamnă că puteți găsi forța centripetă fără viteza tangențială folosind ecuația obișnuită pentru forța gravitațională:
F = Gm1m2 / r2
Unde m1 și m2 sunt masele, G este constanta gravitațională și r este separarea dintre cele două mase.
Pentru a calcula forța centripetă fără o rază, aveți nevoie fie de mai multe informații (circumferința cercului legată de rază cu C = 2π_r, de exemplu) sau valoarea pentru accelerarea centripetă. Dacă știți accelerația centripetară, puteți calcula forța centripetă direct folosind a doua lege a lui Newton, _F = ma.