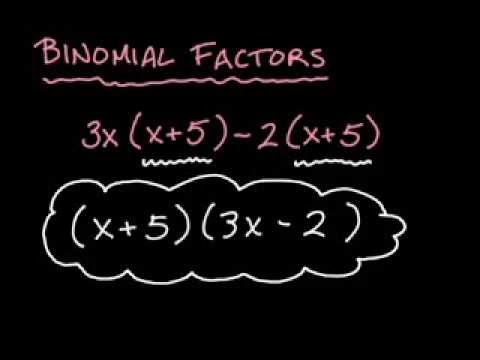
Conţinut
Polinomii sunt adesea produsul unor factori polinomiali mai mici. Factorii binomiali sunt factori polinomi care au exact doi termeni. Factorii binomiali sunt interesanți, deoarece binomii sunt ușor de rezolvat, iar rădăcinile factorilor binomiali sunt identici cu rădăcinile polinomului. Factorizarea unui polinom este primul pas pentru a-și găsi rădăcinile.
Graphing
Graficarea unui polinom este un prim pas bun în găsirea factorilor săi. Punctele în care curba grafoasă traversează axa X sunt rădăcini ale polinomului. Dacă curba traversează axa în punctul p, atunci p este o rădăcină a polinomului și X - p este un factor al polinomului. Ar trebui să verificați factorii obținuți dintr-un grafic, deoarece este ușor să greșiți o citire dintr-un grafic. De asemenea, este ușor să ratați mai multe rădăcini pe un grafic.
Factorii candidați
Factorii binomului candidat pentru un polinom sunt alcătuiți din combinațiile factorilor primului și ultimului număr din polinom. De exemplu 3X ^ 2 - 18X - 15 are ca prim număr 3, cu factorii 1 și 3, și ca ultim număr 15, cu factorii 1, 3, 5 și 15. Factorii candidați sunt X - 1, X + 1 , X - 3, X + 3, X - 5, X + 5, X - 15, X + 15, 3X - 1, 3X + 1, 3X - 3, 3X + 3, 3X - 5, 3X + 5, 3X - 15 și 3X + 15.
Găsirea factorilor
Încercând fiecare dintre factorii candidați, descoperim că 3X + 3 și X - 5 împart 3X ^ 2 - 18X - 15 fără rest. Deci 3X ^ 2 - 18X - 15 = (3X + 3) (X - 5). Observați că 3X + 3 este un factor pe care l-am fi ratat dacă ne-am baza doar pe grafic. Curba ar traversa axa X la -1, sugerând că X - 1 este un factor. Desigur, este într-adevăr pentru că 3X ^ 2 - 18X - 15 = 3 (X + 1) (X - 5).
Găsirea rădăcinilor
După ce ai factorii binomiali, este ușor să găsești rădăcinile unui polinom - rădăcinile polinomului sunt aceleași cu rădăcinile binomilor. De exemplu, rădăcinile 3X ^ 2 - 18X - 15 = 0 nu sunt evidente, dar dacă știți că 3X ^ 2 - 18X - 15 = (3X + 3) (X - 5), rădăcina 3X + 3 = 0 este X = -1, iar rădăcina lui X - 5 = 0 este X = 5.